La mécanique des planètes : les lois de Kepler

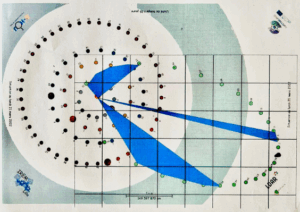
Ce mardi 10 juin, nous avons réalisé un exercice ludique à l’aide d’une bâche représentant une partie du système solaire. Un temps de réflexion nous a été donné, et à l’issu de cela, nous avons déduit la mécanique des planètes et les lois de Kepler.

Sur cette bâche étaient représentés le Soleil, la Terre, Mars, Mercure, Venus et la comète Emcke, ainsi que leurs orbites. Une date et une échelle nous étaient données, soit respectivement le 21 mars 2019 et 1 u.a, unité astronomique (distance Terre-Soleil). Il faut noter que cette valeur n’est pas constante, et correspond à celle de la date indiquée.

L’atelier a commencé par analyser la bâche et les éléments qui la composent. Les orbites des objets célestes se décomposaient en différentes positions (chronophotographie des orbites), avec un écart de temps de 15 jours terrestres. Avec ces données, nous avons pu interpréter les trajectoires orbitales des planètes en imitant leur déplacement. Une personne donnait le tempo en claquant des mains, et à chaque “clap”, nous nous déplacions d’une position dans l’orbite. Par ailleurs, nous avons mesuré à l’aide de cordes les distances entre le Soleil et les planètes à différentes positions pour définir les trajectoires des orbites.

Les expériences nous ont illustré le principe de la première loi de Kepler : les planètes du système solaire ont des orbites sur un plan que l’on appelle “Ecliptique”. Les trajectoires orbitales sont dites “elliptiques”, c’est-à-dire qu’elles ont la forme d’une figure géométrique qui possède deux “centres” appelés foyers. Un des deux foyers des orbites planétaires est le Soleil.

Dans une seconde partie expérimentale, nous avons vérifié notre théorie des trajectoires elliptiques à l’aide d’une corde en supposant que le Soleil était l’un de ces foyers. Puis sur papier à gros carreaux, nous avons mesuré et calculé l’aire approximative de deux surfaces balayées par une même planète pendant une durée égale et avons remarqué que les résultats étaient égaux.

Cette démonstration-ci nous a permis de trouver la seconde loi de Kepler : la loi des aires. Ainsi, pendant des durées égales, les surfaces que balaye le segment Soleil-planète ont des aires égales.

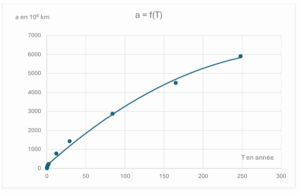
La troisième et dernière loi de Kepler nous a finalement été expliquée graphiquement : le rapport qu’on peut faire entre le temps de révolution T de la planète, et la moitié du grand axe a divisant la trajectoire elliptique de la planète en deux, montée à la puissance 1.5, donne un résultat constant. On peut l’écrire tel que T²⁄a³ = k, avec k une constante.

Graphique 1 : a = f(T)

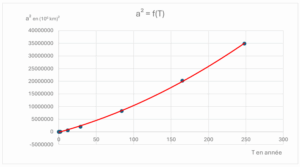
Graphique 2 : a² = f(T)

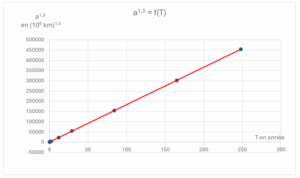
Graphique 3 :   a^1.5 = f(T)

En outre, nous avons pu découvrir les lois de Kepler pour éclaircir notre compréhension de la mécanique planétaire dans notre système, au travers la démonstration d’un jeu ludique et très instructif.

Yahel et Théo